Lausanne, 27 March - 31 March 2017
A. Heatmaps of MNase midpoints (columns 1–2) and DNase I cuts (column 3) surrounding 1000 randomly sampled ChIP-seq peaks for CTCF, NF-kB, Irf4, GABP and C-fos. Heatmap rows are ordered from top to bottom by the nucleosome array log likelihood ratio (LLR). B. Aggregation plot for MNase midpoint and DNase I cutsite depths across all regions and for the subset of regions with LLR>500.
Data re-alignment method
In the current exercise, we will use a simple re-alignment technic, different from the one used in the article but which will complete the expected task. Briefly, this algorithm
will take as input a count matrix where each individual row contains the MNase counts around one given TF binding site. It will then try to re-align each row by comparing them
individually with the data aggregation pattern. Several different shift will be considered and for every one of them, a correlation score will be computed (aggregation pattern
versus the row). The optimal shift for a row will be considered as the one maximizing the correlation. Eventually, the row will be re-aligned according to the corresponding shift.
The code will be provided :-)
In case you are interested, you can check another algorithm developped by the group to discover significant patterns in ChIP-Seq data
[Nair et al., 2014].
In order to identify patterns in MNase dataset around specific transcription factor, we will need two datasets. Instead of using Gaffney and colleagues MNase data, we will use the MNase data generated by the ENCODE Consortium (you can also find Gaffney and colleagues data on our server). Since these data ara coming from GM12878 cells, we will also choose a NFkB peak list coming from the same cell line. The datasets we will need are :
We will use ChIP-Extract Analysis Module to generate a tag count matrix in defined bins around NF-kB sites.
Select the parameters as shown in the picture below and click submit.
Download the Ref SGA File and Table (TEXT) and save as mnase_data_encode.txt.
Navigate into directory containing all the data and launch R.
# A function to realign the data using an iterative process.
# For each individual row of the matrix, for different shifts, a correlation with the
# aggregation pattern of the currently alined data is computed. The shift with the
# highest correlation is kept and the row is shifted accordingly. The whole process
# is performed for a given number of iterations.
# DATA a matrix of counts
# n.shift an integer defining the number of possible shift states
# i.g. with 5 the following shifts are tested : -2,-1,0,1,2
# n.iter the number of iterations to perform
# Returns the realigned data
realign = function(DATA, n.shift, n.iter)
{
# some parameters
n.row = nrow(DATA)
n.col = ncol(DATA)
n.bin = floor(n.shift / 2) # the number of bins to discard on each side of a row to allow the shifts
n.col2 = n.col - n.bin # the right most column with a shift of 0
shift.states = seq(from=0-n.bin, to=0+n.bin)
# output matrix
# DATA.aligned = matrix(data=0, nrow = n.row, ncol=n.col)
DATA.aligned = DATA
# data row coordinates
data.left = n.bin + 1
data.right = n.col - n.bin
# allocate the vector for temp scores only once
SCORES = vector(mode="numeric", length=n.shift)
for(iter in 1:n.iter)
{ REF = colSums(DATA.aligned)
# over all rows
for(i in 1:n.row)
{ # over all possible shifts
for(s in 1:n.shift)
{ # coordinates of the reference pattern for this shift
ref.left = n.bin + shift.states[s] + 1
ref.right = data.right + shift.states[s]
# cannot compute a correlation with a vector of 0 variance
# set the corr to -2 such that it cannot be the maximum score
if(var(DATA[i,ref.left:ref.right]) == 0)
{ SCORES[s] = -2
next
}
# cannot compute a correlation with a covar of 0 -> 0 / x
# set the corr to -2 such that it cannot be the maximum score
if(cov(REF[ref.left:ref.right], DATA[i,data.left:data.right]) == 0)
{ SCORES[s] = -2
next
}
# compute score for the row with this shift
SCORES[s] = cor(REF[ref.left:ref.right], DATA[i,data.left:data.right])
}
# the best alignment is the one with the max score
best = which.max(SCORES)
# compute the coordinates where the row should be inserted in DATA.aligned
out.left = best
out.right = n.col - n.bin + shift.states[best]
# insert the row at the right place
DATA.aligned[i,] = 0
DATA.aligned[i,out.left:out.right] = DATA[i, data.left:data.right]
}
}
# Congrats! you read the code and should be rewarded for this!
# Unfortunatelly, we don't have money... But we may have cake!
# You should get some cake :-)
return(DATA.aligned)
}
DATA = as.matrix(read.table("mnase_data_encode.txt"))
n.shift = 11
n.iter = 10
DATA.aligned = realign(DATA, n.shift, n.iter)
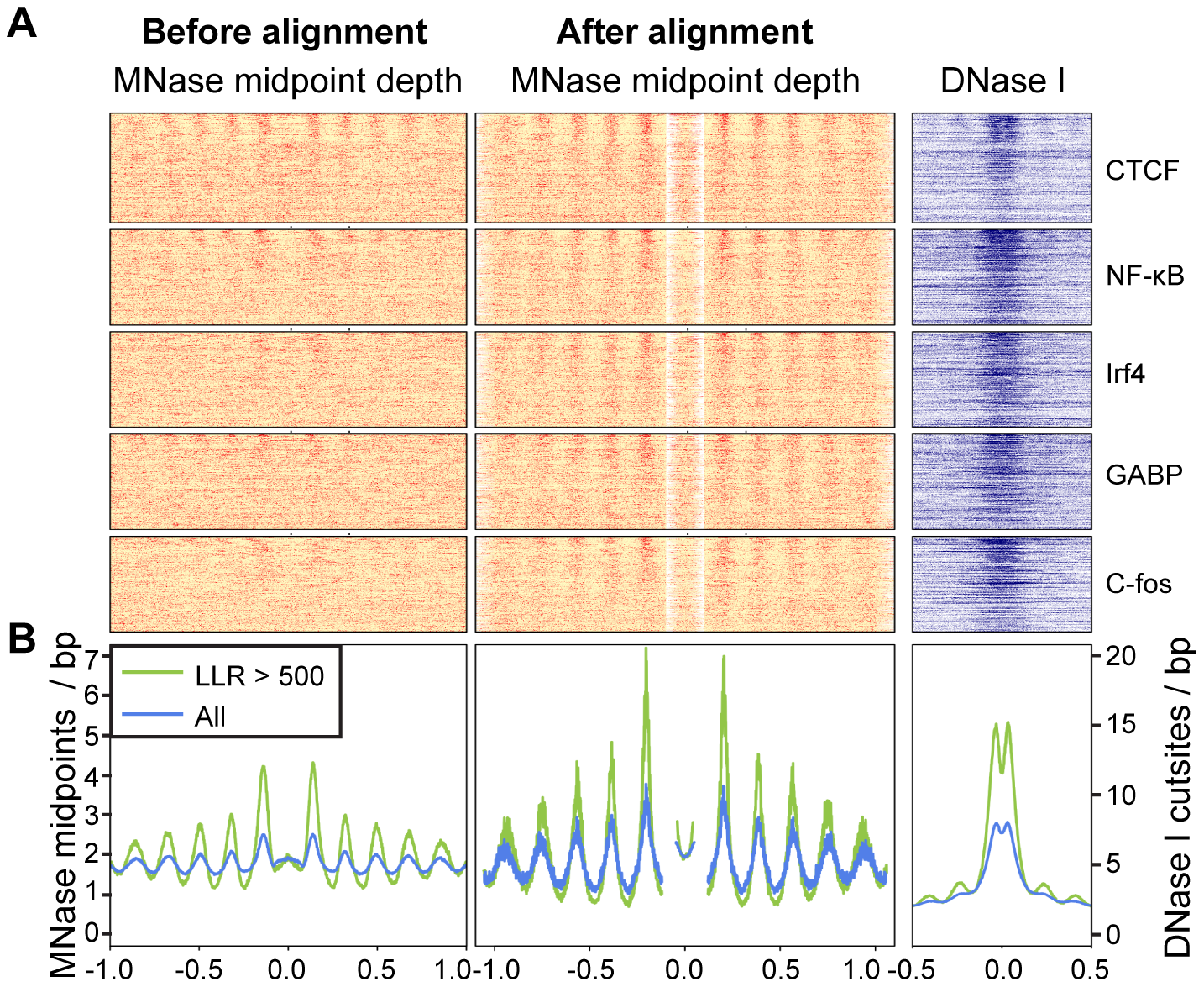
# A function to reorder the rows of a matrix according to the overall
# similarity (correlation) of each row to the column sums of the matrix.
# The top rows will have the highest similarity with the column sums and
# the bottom rows the lowest.
# MATRIX a matrix of numerics of interest
# Returns the same matrix with the rows reordered
order.rows = function(MATRIX)
{ REF = colSums(MATRIX)
SCORES = apply(MATRIX, 1, cor, REF)
ord = order(SCORES, decreasing=F)
return(MATRIX[ord,])
}
# plot
# install package 'zoo' using if needed
# install.packages("zoo")
library(zoo)
color = colorRampPalette(c("white", "red"), space = "rgb")(100)
X = rollapply(order.rows(DATA), width=20, mean, by=20, by.row=TRUE)
Y = rollapply(order.rows(DATA.aligned), width=20, mean, by=20, by.row=TRUE)
layout(matrix(c(1,2,3,4), nrow=2, ncol=2, byrow=T), heights=c(1.5,1.5))
image(t(X), col=color, xaxt="n", yaxt="n", bty="n")
title("Before alignment")
image(t(Y), col=color, xaxt="n", yaxt="n", bty="n")
title("After alignment")
plot(seq(-990, 990, 10), colMeans(DATA), type="l", lwd=2, ylab="", xlab="", bty="n", ylim=c(0,12))
plot(seq(-990, 990, 10), colMeans(DATA.aligned), type="l", lwd=2, ylab="", xlab="", bty="n", ylim=c(0,12))
plot(seq(-990, 990, 10), colSums(DATA.aligned), type="l", lwd=2, ylab="", xlab="", bty="n",col="green", ylim=c(0,1.7))