ChIP-partitioning

Chip-seq data analysis: from quality check to motif discovery and more

Lausanne, 27 April - 1 May 2015

ChIP-partitioning tool: Alignment of MNase tags around NFKB sites

Sunil Kumar and Philipp Bucher

Introduction

Current exercise is baesd on the following paper:

et al.

23166509

A. Heatmaps of MNase midpoints (columns 1–2) and DNase I cuts (column 3) surrounding 1000 randomly sampled ChIP-seq peaks for CTCF, NF-kB, Irf4, GABP and C-fos. Heatmap rows are ordered from top to bottom by the nucleosome array log likelihood ratio (LLR). B. Aggregation plot for MNase midpoint and DNase I cutsite depths across all regions and for the subset of regions with LLR>500.

We will focus on only a part of the figure, and explore the MNase pattern around NF-kB (pre and post 'alignment' or in our case using 'ChIP partitioning' algorithm).

ChIP partitioning method

In the current exercise we will use a probabilistic partitioning methods developed by our group to discover significant patterns in ChIP-Seq data [Nair et al., 2014]. Our methods take into account signal magnitude, shape, strand orientation and shifts. We have compared this methods with some of the existing methods and demonstrated significant improvements, especially with sparse data. Besides pattern discovery and classification, probabilistic partitioning can serve other purposes in ChIP-Seq data analysis.

In the current exercise we will exemplify its merits in the context of peak finding and partitioning of MNase patterns around human transcription factor NF-kB.

Hints and recipes

In order to identify patterns in MNase dataset around specific transcription factor, we will need two datasets.

A custom NFKB peak list from GM12878 cells. In the article, the authors used MACs to perform the peak calling step on ENCODE ChIP-seq data coming from GEO serie GSE31477. Here, we called peaks using ChIP-Peak, our own peak calling tool, on NFkB ChIP-seq reads from GM12891 cells replicate 2 (see the image below). This replicate seemed to be the best of the three replicates when performing cross strand correlations.

A pool of 147bp long MNase fragments from different GM cell lines from GEO serie GSE36979.

We will use ChIP-Extract Analysis Module to generate a tag count matrix in defined bins around NF-kB sites. Select the parameters as shown in the picture below and then click submit. In this case, no centering is used because the MNase data are paired-end.

Download the Ref SGA File and Table (TEXT) and save as mnase_data.txt.

Performing ChIP-partitioning

The code has been taken from the supplementary material of Nair et al., 2014, Probabilistic partitioning methods to find significant patterns in ChIP-Seq data, Bioinformatics, 30, 2406-2013, PMID 24812341.

Navigate into directory containing all the data and launch R.

Load the EM function with shifting: Hide script

em_shape_shift = function(c,q,data) {
   K=dim(c)[1]; L=dim(c)[2]; N=dim(data)[1]; S=dim(q)[2]
   l=array(dim=c(N,K,S)); p=array(dim=c(N,K,S)) 
   for(i in 1:K) {c[i,]=c[i,]/mean(c[i,])}
   rm=matrix(nrow=N, ncol=S)
   for(k in 1:S) {rm[,k] = rowMeans(data[,k:(k+L-1)])}
   for(i in 1:N) { for (j in 1:K) { for (k in 1:S) {
      l[i,j,k]=sum(dpois(data[i,k:(k+L-1)], c[j,] *rm[i,k],log=T)) }}}
   for(i in 1:N) {
      p[i,,] = q*exp(l[i,,]-max(l[i,,])); p[i,,] = p[i,,]/sum(p[i,,])}
   q = apply(p, c(2,3), mean)
   c = 0; for(k in 1:S) {
   c = c + (t(p[,,k]) %*% data[,k:(k+L-1)])}
   c = c/apply(p, 2, sum)
   c <<- c; q <<- q; p <<- p;
   }

reg_shift = function(q) {
   K=dim(q)[1]; S=dim(q)[2]
      m=sum((1:S)*colSums(q))
      s=sum(((1:S)-m)**2*colSums(q))**0.5
   for (i in 1:K) {
      q[i,] = sum(q[i,]) * dnorm(1:S,floor(S/2)+1,s) / sum(dnorm(1:S,floor(S/2)+1,s))
      }
   q <<- q
   }

plot_classes = function(c) {
   K=dim(c)[1]
   if(K == 1) {colors = "black"} else {colors = palette(rainbow(K))}
   for(i in 1:K) {
      if(i != 1) {par(new=T)}
      plot(c[i,], type = "l", ylim=c(0,max(c)), col=colors[i])
      }
   }

Read the data, define input parameters and perform partitioning: Hide script

data=as.matrix(read.table("mnase_data.txt"))

Define classes and shifts:

K=1; S=11; N=dim(data)[1]; L=dim(data)[2]-S+1; ITER=10

Shape based EM partitioning with shifting

mean_shift=floor(S/2)+1
c    = colMeans(data[,mean_shift:(mean_shift+L-1)])
flat = matrix(data=mean(data), nrow=1, ncol=L)
q=q0 = dnorm(1:S,mean_shift,1)/sum(dnorm(1:S,mean_shift,1))
 for (m in 1:K) {
   c = rbind(flat,c)
   q = rbind(q0/m,q); q=q/sum(q) 
   plot_classes(c); print(q)
   for(i in 1:ITER)
   {reg_shift(q); c[1,]=flat;
      em_shape_shift(c,q,data); plot_classes(c); print(q)}
   }

Shift the tags data: Hide script

data_shifted = matrix(0, nrow=dim(data)[1], ncol=L)
start=apply(p[,2,],1,which.max)
for(i in 1:(dim(data)[1])) {
   data_shifted[i,] = data[i,start[i]:(start[i]+L-1)]
   }

P=apply(p[,2,],1,sum)
data_shifted=data_shifted[order(P),]
P_shifted=sort(P)

Plotting the results: Hide script

library(zoo) # install package 'zoo' using install.packages("zoo")
color <- colorRampPalette(c("white", "red"), space = "rgb")(100)
x <- rollapply(data, width=20, mean, by=20, by.row=TRUE)
y <- rollapply(data_shifted, width=20, mean, by=20, by.row=TRUE)
layout(matrix(c(1,2,3,4), nrow=2, ncol=2), heights=c(1.5,1.5))
par(mar=c(0,5,0,0.5), oma=c(5,0,2,0))
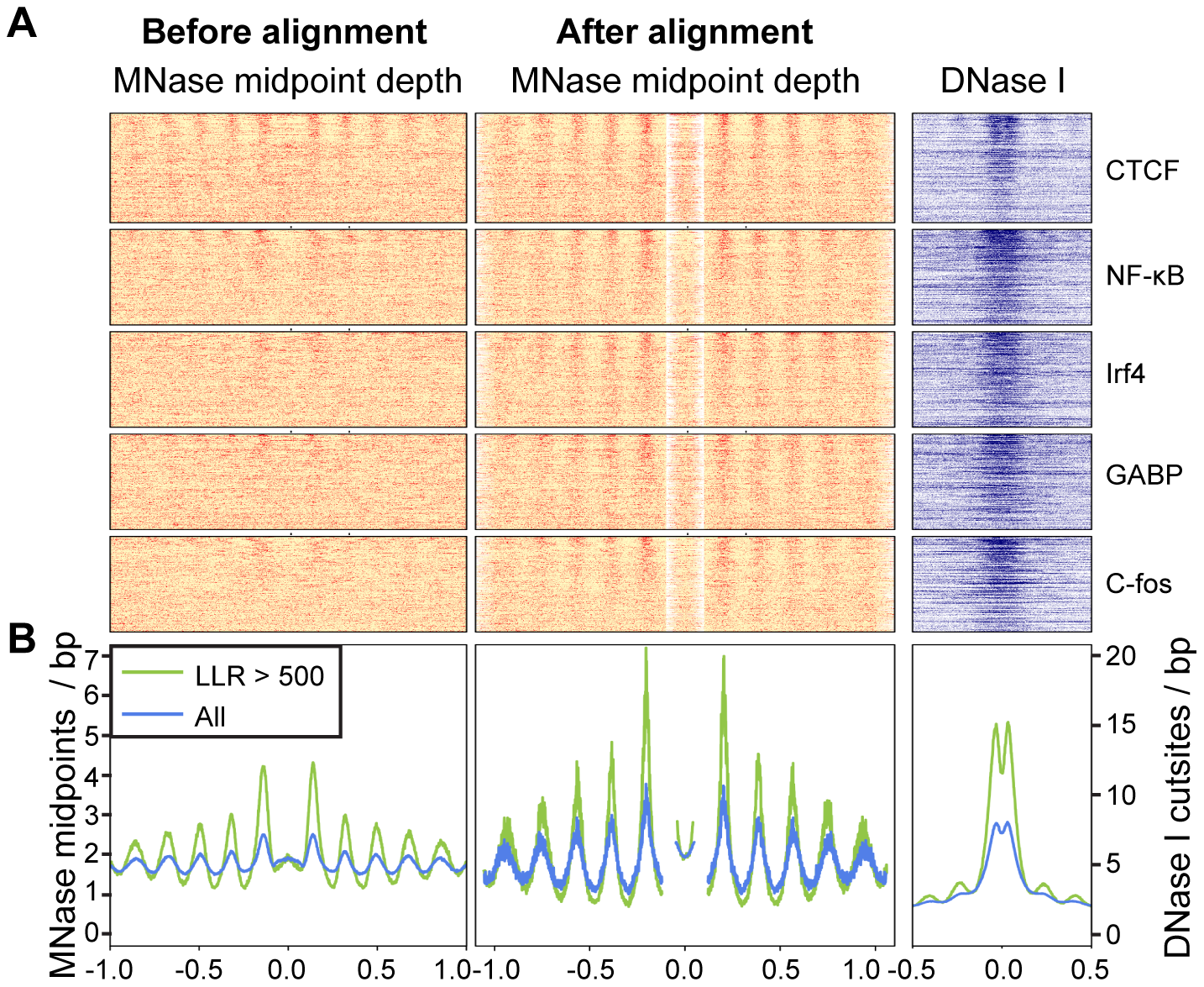
image(t(x), col=color, xaxt="n", yaxt="n", bty="n")
plot(seq(-990, 990, 10), colMeans(data), type="l", lwd=2, ylab="", xlab="", bty="n", ylim=c(0,0.4))
image(t(y), col=color, xaxt="n", yaxt="n", bty="n")
plot(seq(-940, 940, 10), colMeans(data_shifted), type="l", lwd=2, ylab="", xlab="", bty="n",col="blue", ylim=c(0,0.4))
par(new=T)
plot(seq(-940, 940, 10), colSums(data_shifted*P_shifted)/sum(P_shifted), type="l", lwd=2, ylab="", xlab="", bty="n",col="green", ylim=c(0,0.4))
legend("topleft", legend=c("class 1","ALL"), lty=1, col=c("green", "blue"), bty="n", lwd=c(5,5))